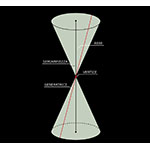
In generale le sezioni coniche – o, più in breve, le coniche – sono la famiglia di curve ottenibili tagliando con piani variamente inclinati un cono circolare: una superficie a due falde generata dalla rotazione attorno a una retta, detta asse, di una seconda retta, chiamata generatrice, che interseca l'asse in un punto (il vertice del cono) ed è inclinata rispetto all'asse di un angolo dato (la semiampiezza del cono). Si ritiene che i primi autori a descrivere queste curve e le loro proprietà siano stati Aristeo (IV sec. a.C.) e Euclide (IV-III sec. a.C.). I loro lavori andarono però ben presto perduti, oscurati per fama dall'opera di Apollonio di Perge (seconda metà III sec. a.C.) intitolata Le coniche.

Quando si taglia un cono circolare con un piano perpendicolare al suo asse, si ottiene (per definizione) una circonferenza. Questa conica particolare è altrimenti nota come l'insieme dei punti del piano equidistanti da un punto dato: il centro della circonferenza.

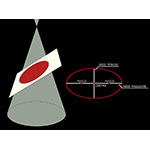
Se si taglia un cono circolare con un piano inclinato rispetto al suo asse più della generatrice, si ottiene una curva chiusa detta ellisse. La curva assomiglia a una circonferenza quanto più il piano tende a essere perpendicolare rispetto all'asse; viceversa la curva s'allunga sempre più quando l'inclinazione del piano tende a quella della generatrice. L'ellisse possiede due assi di simmetria perpendicolari fra loro, il cui punto d'incontro si chiama centro dell'ellisse. Poiché ai due assi corrispondono la larghezza massima e la larghezza minima della curva, essi vengono designati rispettivamente come asse maggiore e asse minore. Sul maggiore, in posizioni opposte e simmetriche rispetto al centro, si trovano due punti particolari: i fuochi dell'ellisse. Rispetto ai fuochi l'ellisse può essere definita anche come luogo geometrico: l'insieme dei punti del piano la cui somma delle distanze dai fuochi è sempre uguale a una costante data (maggiore della distanza tra i fuochi).

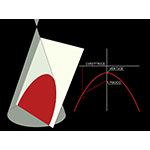
È la curva aperta ricavabile tagliando il cono circolare con un piano parallelo alla generatrice. La parabola possiede un unico asse di simmetria, detto perciò, più semplicemente, asse della parabola. Il punto estremo in cui la curva attraversa l'asse è il vertice della parabola. Opposti e simmetrici rispetto al vertice, si trovano due punti notevoli dell'asse. Il primo, nella concavità della curva, è detto fuoco della parabola; l'altro, all'esterno della concavità, è il punto di minima distanza fra la curva e una retta, perpendicolare all'asse, denominata direttrice della parabola. Rispetto al fuoco e alla direttrice la parabola può essere definita come l'insieme dei punti del piano equidistanti dall'uno e dall'altra.

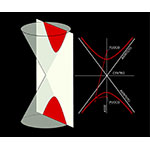
Tagliando il cono circolare a due falde con un piano inclinato rispetto all'asse meno della generatrice, si ottiene su ciascuna falda un ramo della curva nota come iperbole. I due rami sono speculari rispetto a due assi di simmetria perpendicolari fra loro, la cui intersezione si chiama centro dell'iperbole. Sull'asse che taglia l'iperbole, e nella concavità di ciascun ramo, si trovano due punti simmetrici rispetto al centro: i fuochi dell'iperbole. Rispetto a questi ultimi l'iperbole può essere definita anche come luogo geometrico del piano; essa è l'insieme dei punti la cui differenza delle distanze dai fuochi è sempre uguale a una costante data (minore della distanza tra i fuochi). Allontanandosi dal centro, i rami dell'iperbole s'avvicinano indefinitamente, senza mai toccarle, a due rette, dette asintoti. Entrambe le rette passano per il centro dell'iperbole e sono simmetriche rispetto agli assi.