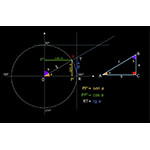
Il rapporto fra due lati di un triangolo dipende dai suoi angoli interni. In altri termini i rapporti fra due lati qualsiasi di un triangolo sono uguali a quelli fra i lati corrispondenti di qualunque triangolo a esso simile.

Forse già nel IV secolo a.C., l'invarianza dei rapporti suggerì ai greci di usare una particolare relazione trigonometrica. Un angolo al centro intercetta due punti sulla circonferenza; il segmento che gli unisce è la corda dell'angolo. Il rapporto fra la corda e il raggio della circonferenza dipende solo dall'angolo al centro e, una volta trovato, può essere tabulato. Nell'Almagesto di Claudio Tolomeo (II secolo d.C.) una tavola delle corde, costruita per ogni mezzo grado in base a un cerchio di raggio 60, permette di conoscere la corda dato l'angolo o, viceversa, l'angolo data la corda.

Per definizione, la corda trovava impiego in problemi dove le figure geometriche erano scomponibili in triangoli isosceli. Verso il VI secolo d.C. gli indiani ritennero più agevole lavorare con triangoli rettangoli e cominciarono a valersi della mezza corda dell'angolo. L'astronomo islamico Muhammad al-Battânî (IX secolo d.C.) chiamò seno dell'angolo la nuova relazione, oggi espressa dal rapporto fra il cateto opposto all'angolo e l'ipotenusa del triangolo rettangolo.

Nel corso del IX secolo gli islamici elaborarono le altre due relazioni trigonometriche fondamentali: il coseno (rapporto fra il cateto adiacente all'angolo e l'ipotenusa) e la tangente (rapporto fra il cateto opposto all'angolo e quello adiacente), nonché le rispettive relazioni reciproche: secante, cosecante e cotangente. Per ciascuna relazione prepararono tavole numeriche accurate da adoperare nella soluzione di problemi pratici.